矩阵与图
线性代数中最被低估的事实:矩阵是图,图是矩阵。
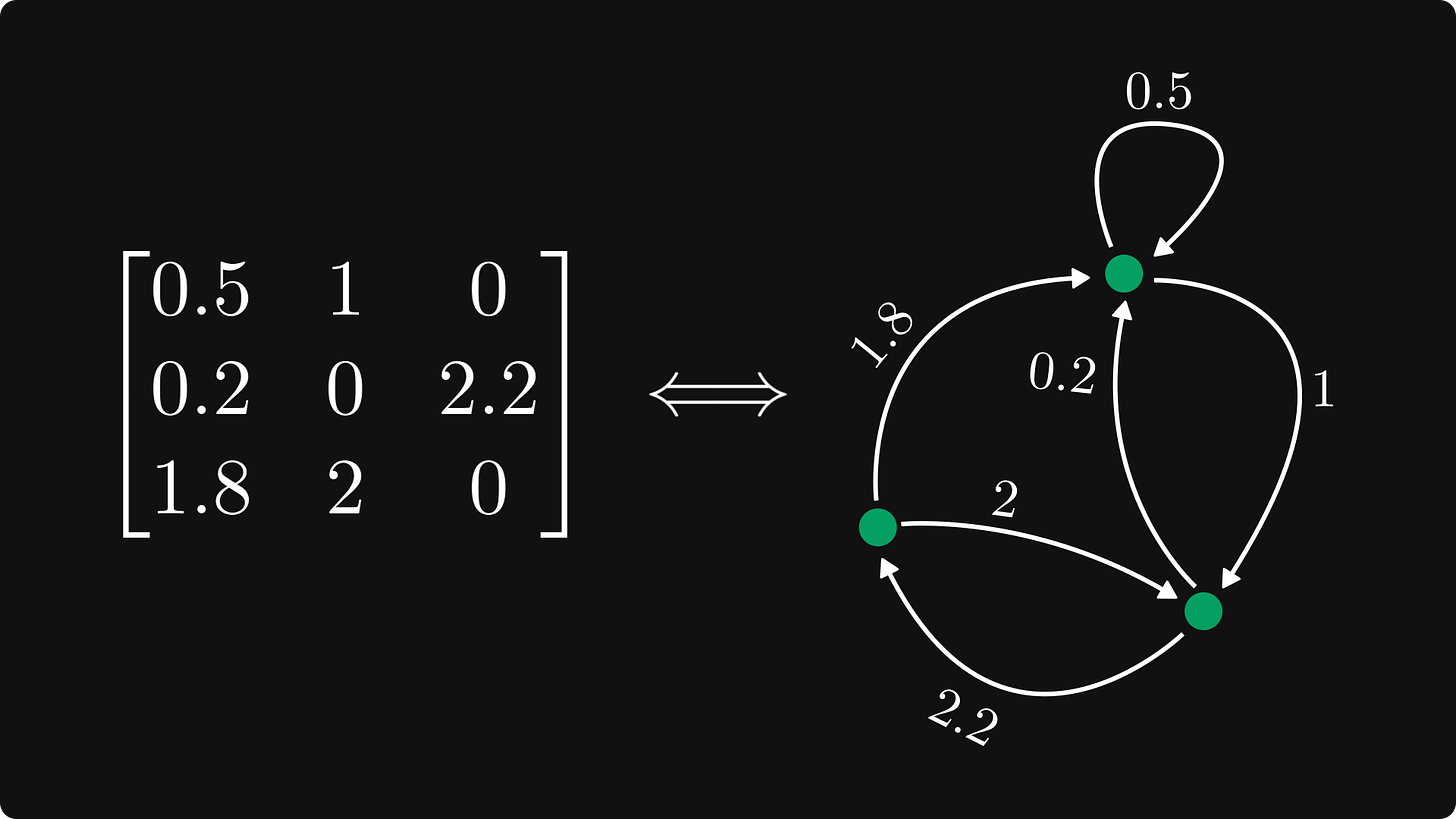
将矩阵转换成图,可以带来一定的便捷性,而且这是一个非常新的视角。
非负矩阵的有向图
矩阵转换层土,规则是这样的:
每一行是一个节点,每个元素代表一个有向且加权的边。值为零的边被省略。第 i 行和 j 列的元素对应于从 i 到 j 的边。
由此生成的图称为该矩阵的有向图(或有向图)。
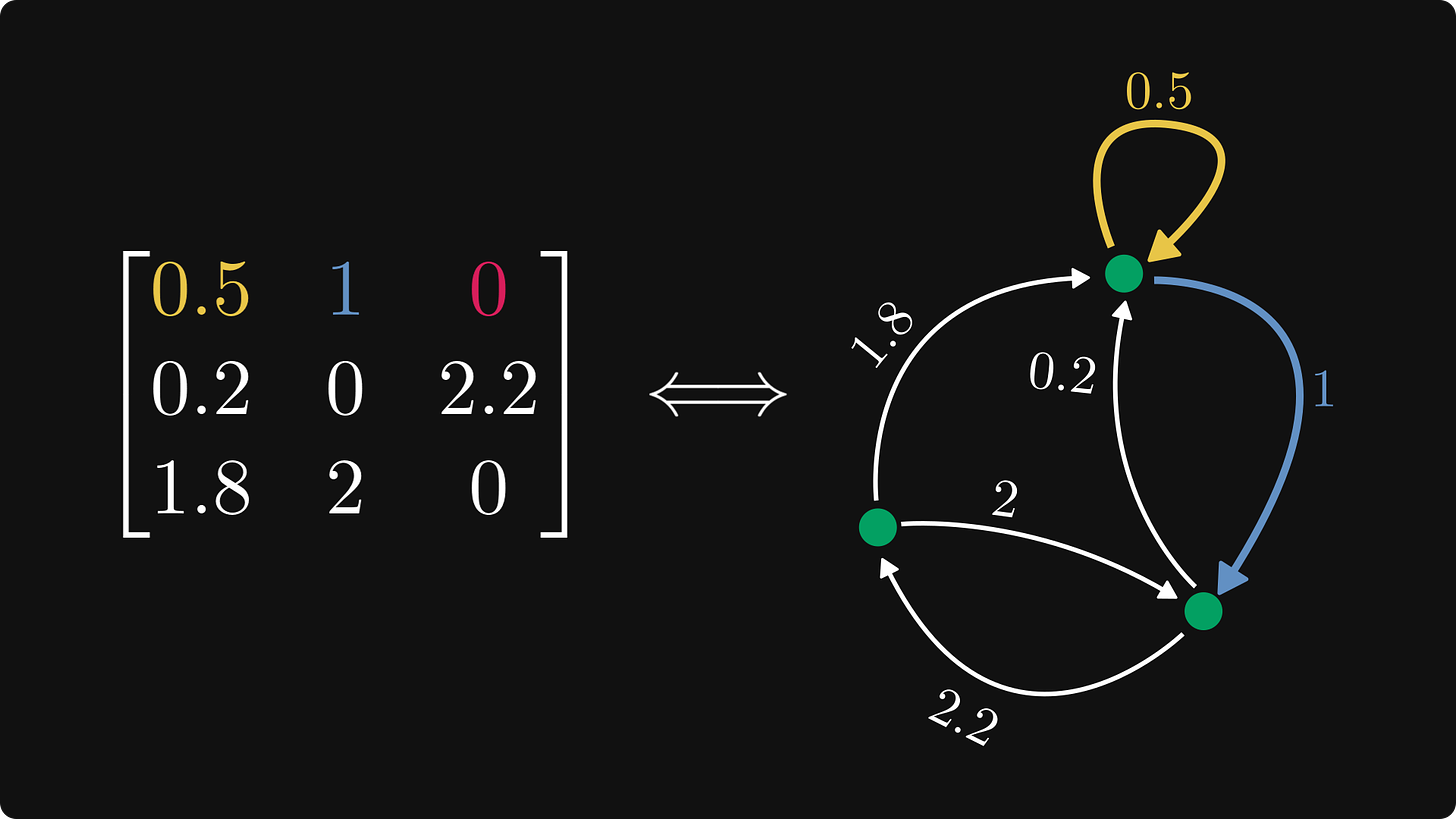
为了更清楚地解释定义,让我们查看第一行,它对应于从第一个节点发出的边。
第一行对应于从第一个节点发出的边
同样,第一列对应于进入第一个节点的边。
第一列对应于进入第一个节点的边
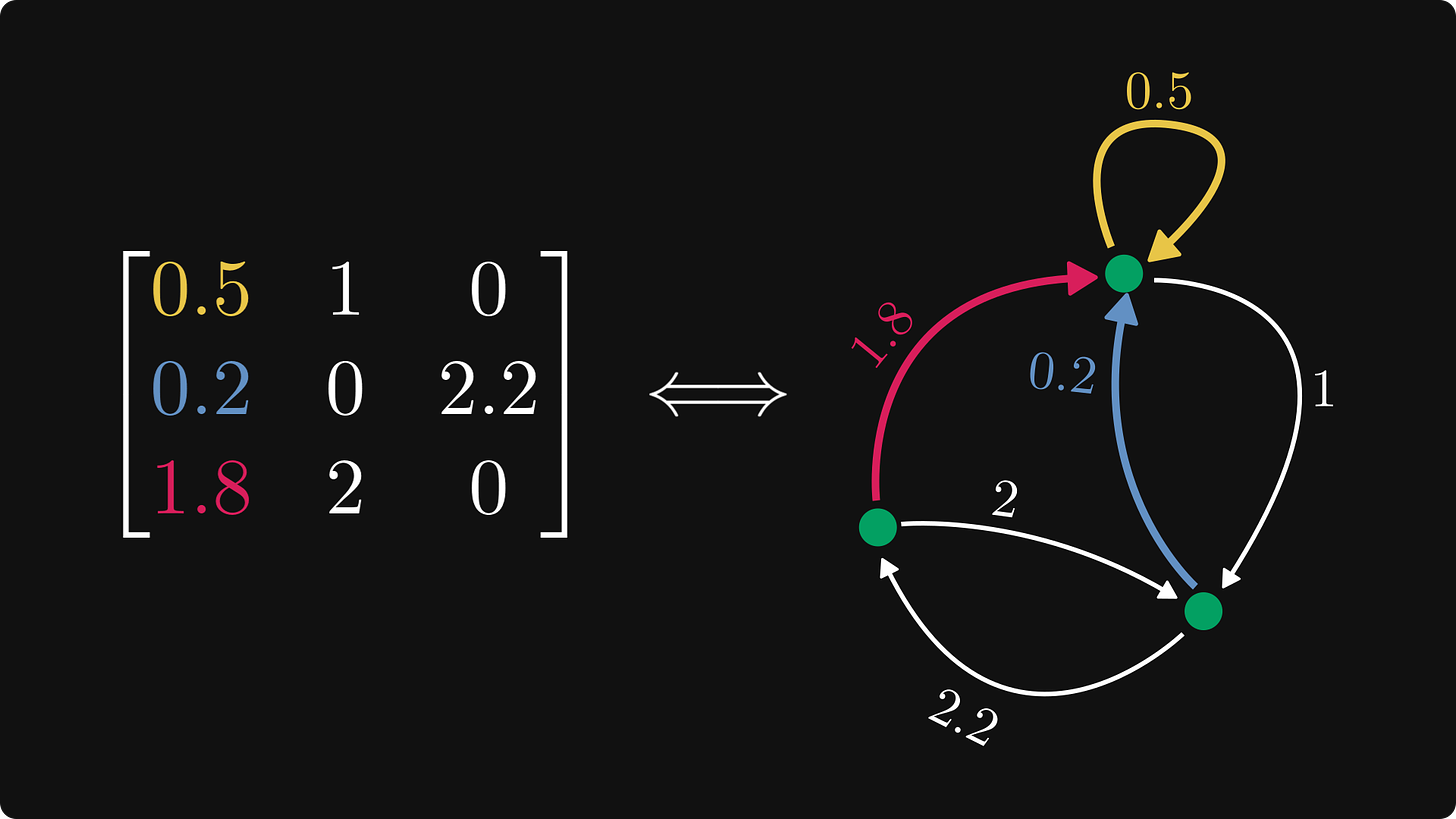
这里是完整的图像,节点标注得很清楚。
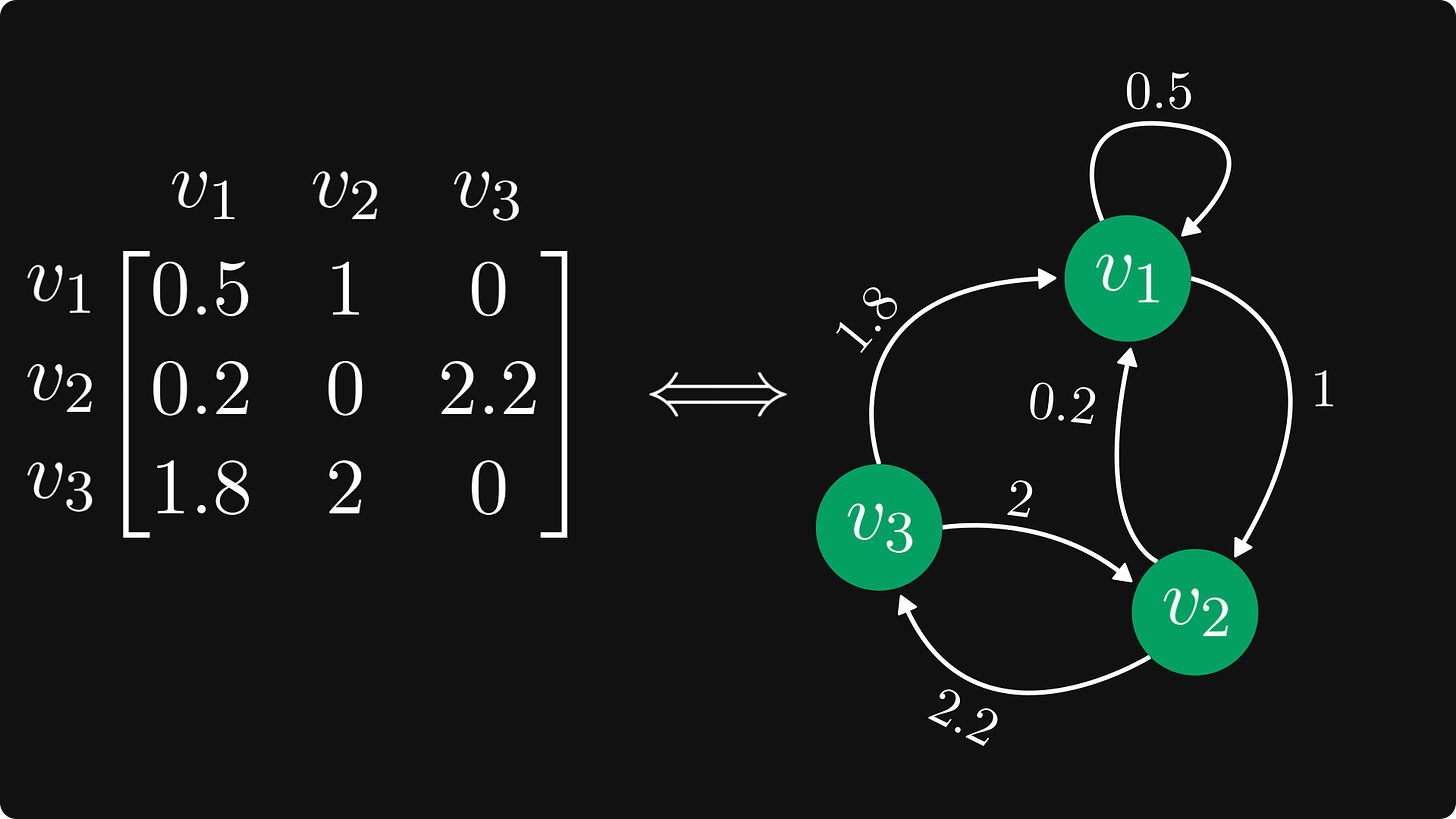
图表示法的优点
为什么有向图表示法对我们有用?
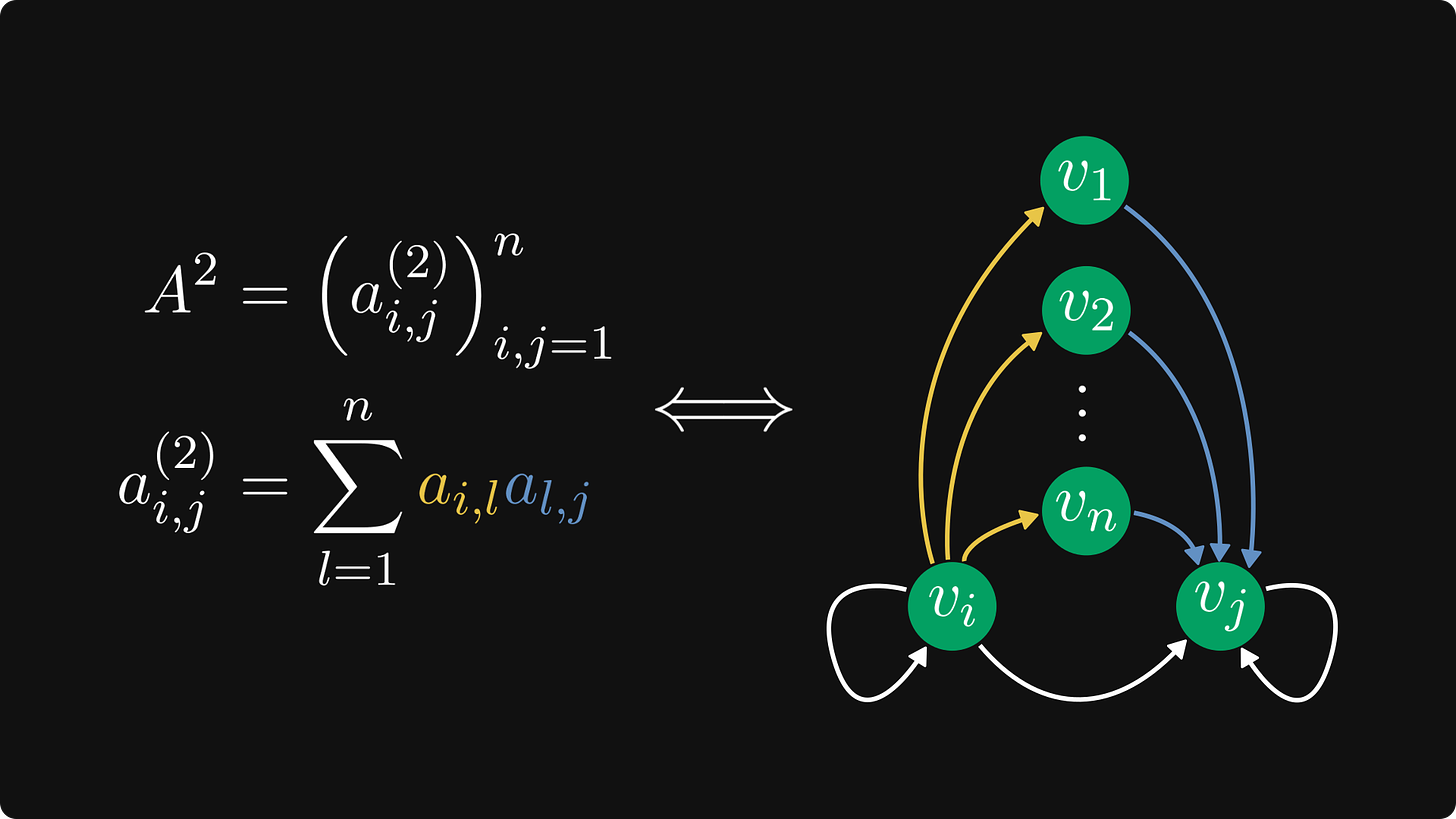
首先,矩阵的幂次对应于图中的路径。
看看平方矩阵的元素。所有可能的两步路径都在定义 A² 元素的和中得到了体现。
矩阵的幂次描述了其有向图上的路径